Aplikasi Limit dalam Kehidupan Sehari - hari
Assalamualaikum Warahmatullahi
Wabarakatuh
Limit juga
dapat digunakan untuk mencari garis singgung suatu kurva di suatu titik
tertentu. Selain itu, konsep limit dapat digunakan untuk menghitung pendekatan
nilai di suatu titik atau masalah-masalah yang tidak mungkin mencapai nilai
ideal, tetapi hanya mendekati saja, misalnya kuota internet yang bertuliskan 2 gigabyte.
Pada kenyataannya, kuota itu tidak tepat 2 gigabyte, melainkan hanya
mendekati 2 gigabyte.
Pemahaman
tentang konsep limit fungsi di suatu titik dan kekontinuan fungsi merupakan
dasar untuk memahami konsep aplikasi limit dalam kehidupan sehari-hari.
Perhatikan grafik fungsi pada gambar berikut ini:
Jika diketahui dua titik, misalnya (x1, y1)
dan (x2, y2). Laju perubahan rata-rata
nilai fungsi didefinisikan sebagai perubahan nilai fungsi y terhadap
nilai fungsi x.
Perhatikan kembali gambar di atas. Dari gambar dapat diketahui bahwa:
x1 = c
x2 = c + h
y1 = f(c)
y2 = f (c + h)
x2 = c + h
y1 = f(c)
y2 = f (c + h)
Dengan
demikian, laju perubahan rata-rata nilai fungsi tersebut adalah:
∆y∆ x= f (c+h) – f (c) . c+h−c = f(c+h) – f(c) h
Jika h → 0, maka A dan B akan
berimpit di x = c. Dengan demikian, diperoleh laju perubahan
sesaat nilai fungsi y = f (x) di x = c,
yaitu :
Secara umum, dapat dituliskan sebagai:
Untuk lebih jelasnya, mari cermati contoh-contoh cara perhitungannya berikut ini
Bisa di dapatkan dengan klik tulisan ini yaaa ⇓⇓⇓
Terimakasih ............... JJJ
Wassalamu'alaikum Warahmatullahi Wabarakatuh
Wassalamu'alaikum Warahmatullahi Wabarakatuh



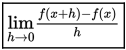


Komentar
Posting Komentar